5.3. pyopus.problems.mgh — More-Garbow-Hillstrom set of test functions¶
More-Garbow-Hillstrom test functions with first derivatives (PyOPUS subsystem name: MGH)
Translated from MATLAB implementation (with bugs omitted).
All test functions in this module are maps from 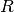 to
to 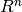 .
Every function is comprised of m auxiliary functions
.
Every function is comprised of m auxiliary functions
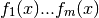
where x is a n-dimensional vector.
The actual test function is then constructed as
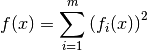
The i-th component of the function’s gradient can be expressed as
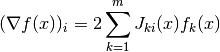
where J(x) is the Jacobian matrix of the auxiliary functions at x where the first index corresponds to the auxiliary function and the second index corresponds to the component of auxiliary function’s gradient.
An exception is the McKinnon function which is not part of the original test suite but is included here because it is a well known counterexample for the Nelder-Mead simplex algorithm. Another exception is the Gao-Han almost quadratic function.
The functions were first published as a test suite in [mgh]. Later bounds were added to most test functions in [gay].
If a function’s documentation does not say anything about bounds, the bounds are defined for all allowed values of n.
This module is independent of PyOPUS, meaning that it can be taken as is and used as a module in some other package. It depends only on the cpi module.
| [mgh] | More J.J, Garbow B. S., Hillstrom K. E.: Testing Unconstrained Optimization Software. ACM Transactions on Mathematical Software, vol. 7, pp. 17-41, 1981. |
| [gay] | Gay D. M., A trust-region approach to linearly constrained optimization. Numerical Analysis (Griffiths, D.F., ed.), Lecture Notes in Mathematics 1066, pp. 72-105, Springer, Berlin, 1984. |
- class pyopus.problems.mgh.MGH(n=2, m=2)¶
Base class for test functions
The initial point can be obtained from the initial member. The full name of the problem is in the name member.
The xl and xh members specify the lower and the upper bound given by D. M. Gay in his paper. If they are None no known lower or upper bound is available in the literature.
Objects of this class are callable. The calling convention is
object(x, gradients)
where x is the input values vector and gradients is a boolean flag specifying whether the Jacobian should be evaluated. The values of the auxiliary functions and the jacobian are stored in the fi and J members.
To create an instance of the extended Rosenbrock function with n=m=4 and evaluate the function and the gradient at the initial point one should:
from pyopus.optimizer.mgh import ExtendedRosenbrock rb=ExtendedRosenbrock(n=4, m=4) (f, g)=rb.fg(rb.initial)
- cpi(bounds=False)¶
Returns the common problem interface.
If bounds is True the bounds defined by Gay are included. Best known minimum information is missing for some problems.
The info member of the returned dictionary is itself a dictionary with the following members:
- m - m parameter of the MGH problem
See the CPI class for more information.
- f(x)¶
Returns the value of the test function at x.
- fg(x)¶
Returns a tuple of the form (f, g) where f is the function value at x and g is the corresponding value of the function’s gradient.
- g(x)¶
Returns the value of the gradient at x.
- name = None¶
The name of the test function
- pyopus.problems.mgh.MGHsuite = [<class 'pyopus.problems.mgh.Rosenbrock'>, <class 'pyopus.problems.mgh.FreudensteinAndRoth'>, <class 'pyopus.problems.mgh.PowellBadlyScaled'>, <class 'pyopus.problems.mgh.BrownBadlyScaled'>, <class 'pyopus.problems.mgh.Beale'>, <class 'pyopus.problems.mgh.JennrichAndSampson'>, <class 'pyopus.problems.mgh.HelicalValley'>, <class 'pyopus.problems.mgh.Bard'>, <class 'pyopus.problems.mgh.Gaussian'>, <class 'pyopus.problems.mgh.Meyer'>, <class 'pyopus.problems.mgh.GulfResearchAndDevelopement'>, <class 'pyopus.problems.mgh.Box3D'>, <class 'pyopus.problems.mgh.PowellSingular'>, <class 'pyopus.problems.mgh.Wood'>, <class 'pyopus.problems.mgh.KowalikAndOsborne'>, <class 'pyopus.problems.mgh.BrownAndDennis'>, <class 'pyopus.problems.mgh.Osborne1'>, <class 'pyopus.problems.mgh.BiggsEXP6'>, <class 'pyopus.problems.mgh.Osborne2'>, <class 'pyopus.problems.mgh.Watson'>, <class 'pyopus.problems.mgh.ExtendedRosenbrock'>, <class 'pyopus.problems.mgh.ExtendedPowellSingular'>, <class 'pyopus.problems.mgh.PenaltyI'>, <class 'pyopus.problems.mgh.PenaltyII'>, <class 'pyopus.problems.mgh.VariablyDimensioned'>, <class 'pyopus.problems.mgh.Trigonometric'>, <class 'pyopus.problems.mgh.BrownAlmostLinear'>, <class 'pyopus.problems.mgh.DiscreteBoundaryValue'>, <class 'pyopus.problems.mgh.DiscreteIntegralEquation'>, <class 'pyopus.problems.mgh.BroydenTridiagonal'>, <class 'pyopus.problems.mgh.BroydenBanded'>, <class 'pyopus.problems.mgh.LinearFullRank'>, <class 'pyopus.problems.mgh.LinearRank1'>, <class 'pyopus.problems.mgh.LinearRank1ZeroColumnsAndRows'>, <class 'pyopus.problems.mgh.Chebyquad'>, <class 'pyopus.problems.mgh.Quadratic'>, <class 'pyopus.problems.mgh.McKinnon'>, <class 'pyopus.problems.mgh.GaoHanAlmostQuadratic'>, <class 'pyopus.problems.mgh.Dixon'>, <class 'pyopus.problems.mgh.OrenPower'>]¶
A list holding references to all function classes in this module.
- class pyopus.problems.mgh.Rosenbrock(n=2, m=2)¶
Rosenbrock test function (n=m=2).
See the MGH class for more details.
- class pyopus.problems.mgh.FreudensteinAndRoth(n=2, m=2)¶
Freudenstein and Roth test function (n=m=2).
See the MGH class for more details.
- class pyopus.problems.mgh.PowellBadlyScaled(n=2, m=2)¶
Powell badly scaled test function (n=m=2).
See the MGH class for more details.
- class pyopus.problems.mgh.BrownBadlyScaled(n=2, m=3)¶
Brown test function (n=2, m=3).
See the MGH class for more details.
- class pyopus.problems.mgh.Beale(n=2, m=3)¶
Beale test function (n=2, m=3).
See the MGH class for more details.
- class pyopus.problems.mgh.JennrichAndSampson(n=2, m=10)¶
Jennrich and Sampson test function (n=2, m>=n).
See the MGH class for more details.
- class pyopus.problems.mgh.HelicalValley(n=3, m=3)¶
Helical valley test function (n=m=3).
See the MGH class for more details.
- class pyopus.problems.mgh.Bard(n=3, m=15)¶
Bard test function (n=3, m=15).
See the MGH class for more details.
- class pyopus.problems.mgh.Gaussian(n=3, m=15)¶
Gaussian test function (n=3, m=15).
See the MGH class for more details.
- class pyopus.problems.mgh.Meyer(n=3, m=16)¶
Meyer test function (n=3, m=16).
See the MGH class for more details.
- class pyopus.problems.mgh.GulfResearchAndDevelopement(n=3, m=3)¶
Gulf research and developement test function (n=3, n<=m<=100).
See the MGH class for more details.
- class pyopus.problems.mgh.Box3D(n=3, m=10)¶
Box 3D test function (n=3, m>=n).
See the MGH class for more details.
- class pyopus.problems.mgh.PowellSingular(n=4, m=4)¶
Powell singular test function (n=m=4).
See the MGH class for more details.
- class pyopus.problems.mgh.Wood(n=4, m=6)¶
Wood test function (n=4, m=6).
See the MGH class for more details.
- class pyopus.problems.mgh.KowalikAndOsborne(n=4, m=11)¶
Kowalik and Osborne test function (n=4, m=11).
See the MGH class for more details.
- class pyopus.problems.mgh.BrownAndDennis(n=4, m=20)¶
Brown and Dennis test function (n=4, m=20).
See the MGH class for more details.
- class pyopus.problems.mgh.Osborne1(n=5, m=33)¶
Osborner 1 test function (n=5, m=33).
See the MGH class for more details.
- class pyopus.problems.mgh.BiggsEXP6(n=6, m=13)¶
Biggs EXP6 test function (n=6, m>=n).
See the MGH class for more details.
- class pyopus.problems.mgh.Osborne2(n=11, m=65)¶
Osborner 2 test function (n=11, m=65).
See the MGH class for more details.
- class pyopus.problems.mgh.Watson(n=6, m=31)¶
Watson test function (2<=n<=31, m=31).
Bounds defined for n=2, 9, and 12.
See the MGH class for more details.
- class pyopus.problems.mgh.ExtendedRosenbrock(n=2, m=None)¶
Extended Rosenbrock test function (n=2k>=2, m=n).
See the MGH class for more details.
- class pyopus.problems.mgh.ExtendedPowellSingular(n=4, m=None)¶
Extended Powell singular test function (n=4k>=4, m=n).
See the MGH class for more details.
- class pyopus.problems.mgh.PenaltyI(n=4, m=None)¶
Penalty I test function (m=n+1).
Bounds defined for n=10.
See the MGH class for more details.
- class pyopus.problems.mgh.PenaltyII(n=4, m=None)¶
Penalty II test function (m=2n).
Bounds defined for n=1, 4, and 10.
See the MGH class for more details.
- class pyopus.problems.mgh.VariablyDimensioned(n=8, m=None)¶
Variably dimensional test function (m=n+2).
Bounds defined for n=10.
See the MGH class for more details.
- class pyopus.problems.mgh.Trigonometric(n=10, m=None)¶
Trigonometric test function (m=n).
Bounds defined for n=10.
See the MGH class for more details.
- class pyopus.problems.mgh.BrownAlmostLinear(n=5, m=None)¶
Brown almost linear test function (m=n).
Bounds defined for n=10k.
See the MGH class for more details.
- class pyopus.problems.mgh.DiscreteBoundaryValue(n=5, m=None)¶
Discrete boundary value test function (m=n).
No bounds defined.
See the MGH class for more details.
- class pyopus.problems.mgh.DiscreteIntegralEquation(n=5, m=None)¶
Discrete integral equation test function (m=n).
No boundas defined.
See the MGH class for more details.
- class pyopus.problems.mgh.BroydenTridiagonal(n=5, m=None)¶
Broyden tridiagonal test function (m=n).
No bounds defined.
See the MGH class for more details.
- class pyopus.problems.mgh.BroydenBanded(n=5, m=None)¶
Broyden banded test function (m=n).
No bounds defined.
See the MGH class for more details.
- class pyopus.problems.mgh.LinearFullRank(n=5, m=None)¶
Linear full rank test function (m>=n). Default m=n.
Bounds defined for n=5.
See the MGH class for more details.
- class pyopus.problems.mgh.LinearRank1(n=5, m=None)¶
Linear rank 1 test function (m>=n). Default m=n.
Bounds defined for n=5.
See the MGH class for more details.
- class pyopus.problems.mgh.LinearRank1ZeroColumnsAndRows(n=5, m=None)¶
Linear rank 1 zero columns and rows test function (m>=n). Default m=n.
Bounds defined for n=5.
See the MGH class for more details.
- class pyopus.problems.mgh.Chebyquad(n=7, m=None)¶
Chebyquad test function (m>=n). Default m=n.
Bounds defined for n=1, 7, 8, 9, and 10.
See the MGH class for more details.
- class pyopus.problems.mgh.Quadratic(n=2, m=None)¶
Quadratic test function (m=n).
See the MGH class for more details.
- class pyopus.problems.mgh.McKinnon(n=2, m=1)¶
McKinnon test function (n=2, m=1).
Does not calculate Jacobian, does not calculate auxiliary functions. Evaluates function and gradient in one step.
McKinnon, K. I. M.: Convergence of the Nelder-Mead Simplex Method to a Nonstationary Point. SIAM Journal on Optimization, vol. 9, pp. 148-158, 1998.
See the MGH class for more details.
- class pyopus.problems.mgh.GaoHanAlmostQuadratic(n=2, m=None, epsilon=0.05, sigma=0.0001)¶
Gao-Han almost quadratic function. m is not used. epsilon and sigma must not be negative.
Function is shifted so that the solution for epsilon=sigma=0 is at [1,1, ..., 1].
Does not calculate Jacobian, does not calculate auxiliary functions. Evaluates function and gradient in one step.
Gao, F., Han., L.: Implementing the Nelder-Mead simplex algorithm with adaptive parameters. Computational Optimization and Applications, vol 51, pp. 259-277, 2012.
See the MGH class for more details.
- class pyopus.problems.mgh.HilbertQuadratic(n=2, m=None)¶
Quadratic function with Hilbert matrix for Hessian. Does not depend on m.
Does not calculate Jacobian, does not calculate auxiliary functions. Evaluates function and gradient in one step.
See the MGH class for more details.
- class pyopus.problems.mgh.Dixon(n=10, m=11)¶
Dixon function. Minimum is at [1, 1, ..., 1].
M.A. Wolfe, C. Viazminsky, Supermemory descent methods for unconstrained minimization, Journal of Optimization Theory and Applications 18 (1976) 455-469.
See the MGH class for more details.
- class pyopus.problems.mgh.OrenPower(n=2, m=None)¶
Oren’s power function. Minimum is at [0, 0, ..., 0].
E. Spedicato, Computational experience with quasi-Newton algorithms for minimization problems of moderately large size, Report CISE-N-175, CISE Documentation Series, Segrato, 1975.
Definition from D. F. Shanno, Kang-Hoh Phua, Matrix conditioning and nonlinear optimization, Mathematical Programming, Volume 14, Issue 1, 1978, pp 149-160.
See the MGH class for more details.