5.2. `pyopus.problems.glbc` — Global optimization test functions¶

Inheritance diagram of pyopus.problems.glbc

Global optimization bound constrained test problems (PyOPUS subsystem name: GLBC)

Implemented by Árpád Bűrmen and Jernej Olenšek.

All test functions in this module are maps from 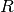$R$ to $R^n$ .

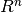Gradient is not implemented and is in some cases even impossible to implement (e.g. Quartic noisy function).

The functions can be wrapped into RandomDelay objects to introduce a random delay in function evaluation.

The Yao et. al. set and the Hedar set have some functions in common. The “Hump” function from the Hedar set is named “SixHump” here. Hedar’s version of the Rosenbrock problem is obtained by setting hedar to True.

The Yang set of test functions extends the Easom’s function to n dimensions. The Zakharov test function is extended beyond K=2. Yang’s version of problems is obtained by setting yang to True. Equality constrained function is omitted (nonlinear equality constraint). Both stochastic functions are also omitted.

The functions were taken from [yao], [hedar], and [yang].

This module is independent of PyOPUS, meaning that it can be taken as is and used as a module in some other package. It depends only on the cpi module.

[yao]

Yao X., Liu Y., Lin G.: Evolutionary programming made faster. IEEE Transactions on Evolutionary Computation, vol. 3, pp. 82-102, 1999.

[hedar]

Hedar A.: Global optimization test problems. http://www-optima.amp.i.kyoto-u.ac.jp/member/student/hedar/Hedar_files/TestGO.htm

[yang]

Yang X.-S.: Test Problems in Optimization. arXiv preprint at http://arxiv.org/abs/1008.0549, 2010.

class pyopus.problems.glbc.GlobalProblem(n)¶

Base class for global optimization test functions

The full name of the problem is in the name member. The lower and the upper bounds are in the xl and xh member.

The position and the function value for the best known solution are given by xmin and fmin.

Objects of this class are callable. The calling convention is

object(x)

where x is the input values vector. The function value at x is returned.

Most functions are variably dimensional (n can be specified as an argument to the constructor).

Example: create an instance of the Schwefel C function with n=40 and evaluate it at the origin:

from pyopus.optimizer.glbc import SchwefelC
from numpy import zeros

sc=SchwefelC(n=40)

# Evaluate the function at the origin
f=sc(zeros(40))

cpi()¶

Returns the common problem interface.

Initial point and gradient function are not available.

See the CPI class for more information.

pyopus.problems.glbc.GlobalBCsuite = [<class 'pyopus.problems.glbc.Quadratic'>, <class 'pyopus.problems.glbc.SchwefelA'>, <class 'pyopus.problems.glbc.SchwefelB'>, <class 'pyopus.problems.glbc.SchwefelC'>, <class 'pyopus.problems.glbc.Rosenbrock'>, <class 'pyopus.problems.glbc.Step'>, <class 'pyopus.problems.glbc.QuarticNoisy'>, <class 'pyopus.problems.glbc.SchwefelD'>, <class 'pyopus.problems.glbc.Rastrigin'>, <class 'pyopus.problems.glbc.Ackley'>, <class 'pyopus.problems.glbc.Griewank'>, <class 'pyopus.problems.glbc.Penalty1'>, <class 'pyopus.problems.glbc.Penalty2'>, <class 'pyopus.problems.glbc.ShekelFoxholes'>, <class 'pyopus.problems.glbc.Kowalik'>, <class 'pyopus.problems.glbc.SixHump'>, <class 'pyopus.problems.glbc.Branin'>, <class 'pyopus.problems.glbc.GoldsteinPrice'>, <class 'pyopus.problems.glbc.Hartman'>, <class 'pyopus.problems.glbc.Shekel'>, <class 'pyopus.problems.glbc.Beale'>, <class 'pyopus.problems.glbc.Bohachevsky'>, <class 'pyopus.problems.glbc.Booth'>, <class 'pyopus.problems.glbc.Colville'>, <class 'pyopus.problems.glbc.DixonPrice'>, <class 'pyopus.problems.glbc.Easom'>, <class 'pyopus.problems.glbc.Levy'>, <class 'pyopus.problems.glbc.Matyas'>, <class 'pyopus.problems.glbc.Michalewicz'>, <class 'pyopus.problems.glbc.Perm'>, <class 'pyopus.problems.glbc.Perm0'>, <class 'pyopus.problems.glbc.Powell'>, <class 'pyopus.problems.glbc.PowerSum'>, <class 'pyopus.problems.glbc.Schwefel'>, <class 'pyopus.problems.glbc.Shubert'>, <class 'pyopus.problems.glbc.Sphere'>, <class 'pyopus.problems.glbc.SumSquares'>, <class 'pyopus.problems.glbc.Trid'>, <class 'pyopus.problems.glbc.Zakharov'>, <class 'pyopus.problems.glbc.DifferentPowerSum'>, <class 'pyopus.problems.glbc.Yang1'>, <class 'pyopus.problems.glbc.Yang2'>, <class 'pyopus.problems.glbc.Yang3'>]¶: A list holding references to all function classes in this module.

class pyopus.problems.glbc.Quadratic(n=30)¶

Quadratic function (n>=1).