4.6. pyopus.optimizer.nm — Unconstrained Melder-Mead simplex optimizer

Unconstrained Nelder-Mead optimizer (PyOPUS subsystem name: NMOPT)

A very popular unconstrained optimization algorithm first published in [nm],

Unfortunately no convergence theory is available. There is even a counterexample available showing how the algorithm can fail. See [mck].

[nm]	Nelder, J. A.,Mead, R.: A simplex method for function minimization. Computer Journal, vol. 7, pp. 308-313, 1965.

[mck]

McKinnon, K. I. M.: Convergence of the Nelder-Mead Simplex Method to a Nonstationary Point. SIAM Journal on Optimization, vol. 9, pp. 148-158, 1998.

class pyopus.optimizer.nm.NelderMead(function, debug=0, fstop=None, maxiter=None, reflect=1.0, expand=2.0, outerContract=0.5, innerContract=-0.5, shrink=0.5, reltol=1e-15, ftol=1e-15, xtol=1e-09, simplex=None, looseContraction=False)

Nelder-Mead optimizer class

reflect, expand, outerContract, innerContract, and shrink are step size factors for the reflection, expansion, outer contraction, inner contraction, and shrink step, respectively.

expansion must be above 1. reflection must be greater than 0 and smaller than expansion. outerContraction must be between 0 and 1, while innerContraction must be between -1 and 0. shrink must be between 0 and 1.

reltol is the relative stopping tolerance. ftol and xtol are the absolute stopping tolerances for cost function values at simplex points and simlex side lengths. See the checkFtol() and checkXtol() methods.

simplex is the initial simplex given by a (ndim*+1) times *ndim array where every row corresponds to one simplex point. If simplex is not given an initial simplex is constructed around the initial point *x0. See the buildSimplex() method for details.

If looseContraction is True the acceptance condition for contraction steps requres that the new point is not worse than the worst point. This is the behavior of the original algorithm. If this parameter is False (which is also the default) the new point is accepted if it is better than the worst point.

See the Optimizer class for more information.

buildSimplex(x0, rel=0.05, abs=0.00025)

Builds an initial simplex around point given by a 1-dimensional array x0. rel and abs are used for the relative and absolute simplex size.

The initial simplex has its first point positioned at x0. The i-th point among the remaining ndim points is obtained by movin along the i-th coordinate direction by 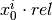or abs if 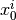is zero.

check()

Checks the optimization algorithm’s settings and raises an exception if something is wrong.

checkFtol()

Checks the function value tolerance and returns True if the function values are within 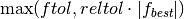of the point with the lowest cost function value ().

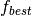checkXtol()

Returns True if the components of points in the simplex are within 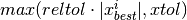of the corresponding components of the point with the lowest cost function value ().

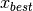orderSimplex()

Reorders the points and the corresponding cost function values of the simplex in such way that the point with the lowest cost function value is the first point in the simplex.

reset(x0)

Puts the optimizer in its initial state and sets the initial point to be the 1-dimensional array x0. The length of the array becomes the dimension of the optimization problem (ndim member).

The initial simplex is built around x0 by calling the buildSimplex() method with default values for the rel and abs arguments.

If x0 is a 2-dimensional array of size (ndim*+1) times *ndim it specifies the initial simplex.

run()

Runs the optimization algorithm.