4.9. pyopus.optimizer.boxcomplex — Box’s constrained simplex optimizer¶

Box’s constrained simplex optimizer (PyOPUS subsystem name: BCOPT)
A version of the Box’s simplex algorithm that is capable of handling box constraints. First published (as a general constrained algorithm) in [box].
Unfortunately no convergence theory is available.
A simplex in the Box’s version of the algorithm is referred to as the complex.
| [box] | Box, M. J.: A new method of constrained optimization and a comparison with other methods. Computer Journal, vol. 8, pp. 42-52, 1965. |
- class pyopus.optimizer.boxcomplex.BoxComplex(function, xlo, xhi, debug=0, fstop=None, maxiter=None, population_factor=2.0, initial_box=1.0, reflection=1.3, contraction=0.5, gamma=1e-05, gamma_stop=None)¶
Box’s constrained simplex optimizer class
population_factor determines the number of points in the automatically generated somplex (population_factor times ndim). The number of points in the complex must be greater than ndim.
initial_box is the relative size (see normalization scale in BoxConstrainedOptimizer class) of the box from which the initial complex points are chosen.
reflection and contraction are the reflection and contraction step coefficients. reflection must be positive and greater than 1. contraction must be between 0 and 1.
gamma specifies the relative distance (with respect to the normalization defined by the bounds) that is considered as close enough. Used in the process of deciding whether one the contractions should be performed towards the best point in the simplex.
gamma_stop is the relative simplex size at which the algorithm stops. If it is not given the value provided as gamma is used.
See the BoxConstrainedOptimizer class for more information.
- buildComplex(x0)¶
Builds an initial complex around point given by a 1-dimensional array x0. The number of points (npts) is determined as the closest integer not exceeding the product of x0 and population_factor.
A box with size equal to the product of
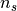 and initial_box
around x0 is created and npts-1 points are chosen randomly from the
box. Together with x0 they form the initial complex.
and initial_box
around x0 is created and npts-1 points are chosen randomly from the
box. Together with x0 they form the initial complex.See the BoxConstrainedOptimizer class for the definition of
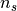 .
.
- check()¶
Checks the optimization algorithm’s settings and raises an exception if something is wrong.
- reset(x0)¶
Puts the optimizer in its initial state and sets the initial point to be the 1-dimensional array or list x0. The length of the array becomes the dimension of the optimization problem (ndim member). The shape of x0 must match that of xlo and xhi. The initial complex is built around x0 by calling the buildComplex() method.
If x0 is a 2-dimensional array or list of size npts times ndim it specifies the initial complex.
- run()¶
Runs the optimization algorithm.